Решение задачи 1.
a) Обозначим оставшиеся на доске числа:
a1<a2<a3<
... <a1001<a1002.
И рассмотрим две строго возрастающие последовательности чисел в промежутке от 1
до 2000:
(1) a2<a3<
... <a1001<a1002
и
(2)
a2–a1<
a3–a1<
... <
a1001–a1<
a1002–a1.
В обеих последовательностях содержится 1001 + 1001 = 2002 числа. Эти
числа не могут быть все различными, т.к. в промежутке от 1 до 2000
всего имеется 2000 различных чисел. Следовательно, существует пара
равных чисел по одному из каждой последовательности:
ak=ap–a1.
Таким образом, среди чисел на доске имеются три числа:
ak,ap и a1
такие, что
a1+ak=ap.
С другой стороны, если первоначально стереть 999 наименьших чисел,
то среди оставшихся 1001 чисел сумма двух наименьших 1000 + 1001 = 2001 уже
превышает наибольшее число на доске.
b) Обозначим оставшиеся на доске числа:
a1<a2<a3<
... <a1910<a1911
и установим два вспомогательных факта.
1. Покажем, что ai ≤89+i для каждого i=1,2,3,…,1911.
Действительно, a1911–ai=
(a1911–a1910)+
(a1910–a1909)+...+
(ai+1–ai)≥1+1+...+1=1911–i.
Следовательно, 2000≥a1911≥ai+
1911–i и 89+i≥ai.
2. Убедимся, что S=a1+a2+
...+a19≤a1792. На самом деле,
a1+a2+
...+a18≤(89+1)+(89+2)+...+(89+18)=1773≤
(a1792–a1791)+...+
(a20–a19)=
(a1792–a19), т.е.
S=a1+a2+
...+a19≤a1792.
3. Теперь, как в пункте а, рассмотрим две строго
возрастающие последовательности чисел в промежутке от 1 до 2000:
(1) a20<a21<
... <a1910<a1911
и
(2) a1793–S<a1794–S<
...<a1911–S, где S=a1
+a2+...+a19.
В обеих последовательностях содержится 1892+119=2011 чисел. Эти числа не
могут быть все различными, т.к. в промежутке от 1 до 2000 всего имеется
2000 различных чисел. Следовательно, существует пара равных чисел по одному
из каждой последовательности: ak=ap–S.
Таким образом, среди чисел на доске имеется 21 число:
a1, a2,...,
a19,
ak,
ap такие, что a1+
a2+...+a19+
ak=ap.
С другой стороны, если первоначально вычеркнуть 90 наименьших чисел, то
сумма двадцати наименьших оставшихся чисел 91+92+...+110=2010 уже превышает
наибольшее число на доске.
Замечание.
Данная задача относится к типу задач на "Принцип
Дирихле"
Вернуться на главную страницу
к текстам
Решение задачи 2.
Рассмотрим 19 разностей соседних чисел:
a2–a1,
a3–a2,...,
a20–a19. Запишем их в порядке
возрастания и обозначим b1≤b2
≤b3≤...≤b19.
Очевидно, что b1+b2+...+b19
=a20–a1≤69.
Теперь допустим, что среди разностей b1,b2,
...b19 нет четырёх одинаковых. Тогда (принцип Дирихле) среди 3k+1
разностей найдётся хотя бы одна превышающая k (k=1,2,3,4,5,6), т.е. k+1≤b3k+1.
Откуда уже получаем 3≤b1+b2+b3,
6≤b4+b5+b6,
9≤b7+b8+b9,
12≤b10+b11+b12,
15≤b13+b14+b15,
18≤b16+b17+b18,
7≤b19. Сложим неравенства 70≤b1+b2+...+b19,
а выше
отмечено, что b1+b2+...+b19≤69.
Противоречие.
Второе решение, которое я нашёл на олимпиаде.
Рассмотрим несколько (окажется 7) возрастающих числовых последовательностей
в промежутке от 1 до 76 (почему 76? Будет ясно позже). В каждой из них будет
20 членов. Вот первая последовательность: a1<a2
<...<a20. Вот вторая последовательность:
a1+1<a2+1<...<a20+1.
Если у этих последовательностей имеются 4 общих члена, то мы уже можем указать 4 разности равные 1.
Теперь будем полагать, что во второй последовательности найдутся по крайней мере 17
новых членов, которых нет в первой последовательности. Пришёл черёд рассмотреть
третью последовательность: a1+2<a2+2<
...<a20+2. Если у новой последовательности найдутся 4 общих члена
с первой или со второй последовательностями, то можем указать 4 разности равные 1 или 2.
Далее будем полагать, что третья последовательность содержит по крайней мере 14 новых членов,
которые не встречаются ни в первой, ни во второй последовательностях. Думаю, что уже понятно,
что будет дальше. Четвёртая последовательность a1+3<a2+3
<...<a20+3 принесёт 11 новых членов, пятая последовательность
– 8 новых членов, шестая последовательность – 5 новых членов и последняя, седьмая,
последовательность – только 2 новых члена. Остаётся заметить, что наибольший член всех
последовательностей (он же последний член седьмой последовательности) a20+6≤76
(вот оно 76!), а количество разных членов 20+17+14+11+8+5+2=77. Противоречие. Итак,
на каком-то этапе найдутся 4 общих члена двух последовательностей, и, следовательно,
некоторая разность (величина её от 1 до 6) повторится 4 раза.
Замечание.
Данная задача, как и первая, относится к типу задач на "Принцип
Дирихле".
Вернуться на главную страницу
к текстам
Решение задачи 3.
1) По принципу Дирихле для нечётного числа m существует число вида 2s–1, которое
делится на m.
2) Пусть a<b - два натуральных числа, причём (a+b) - нечётное число.
Вместо "переливания": (2a, b–a) будем рассматривать числа (2a,2b), но для чисел,
превосходящих a+b (в данном случае – это 2b), будем переходить к их остаткам от
деления на (a + b) (в данном случае: 2b=(a+b)•1+(b – a)).
Итак, получаем последовательность пар (a,b), (2a,2b), (4a,4b),...., (2s-1a,2s-1b),
где s определим (п.1) как наименьшее число такое, что 2s–1
делится на (a+b). Далее продолжать не нужно, т.к. остатки чисел (от деления на (a+b))
в следующих парах будут циклически повторятся. Вывод: если одно из двух первоначальных
чисел имеет вид 2kc, где c - нечётное число, то через несколько шагов придём к c.
3) Пусть теперь a,b,c - данные числа (т.е. объёмы воды). Если их НОД больше 1,
то разделим на него все числа. Если общая сумма чётная, то существует такое переливание,
после которого все числа станут чётными, а тогда снова НОД больше 1, и снова разделим
на него все числа. Теперь можно предположить, что a и b - чётные, c - нечётное:
a=2xp, b=2qq, где p,q - нечётные (для определённости p≥q).
Ввиду п.2 и, используя третье число c (раздельно для a и b), можно перейти a =>
2p, b => 2q. И далее (2p,2q) => (2(p–q),4q). Заметим, что у обоих чётных чисел
их нечётные составляющие не увеличились, а одна даже уменьшилась. Продолжая п.3 несколько
раз мы непременно придём к равным нечётным составляющим, а тогда и к равным числам,
после чего получим один 0.
Вернуться на главную страницу
к текстам
Решение задачи 4.
Обозначим через Ai – множество квадратиков, стороны которых
заключены в промежутке [1/2i;1/2i-1), если i=1,2,3,...,
a для i=0 соответствующий промежуток: [1;бесконечность). Полагаем сначала,
что A0 - пустое множество, иначе покрытие уже существует.
1. Уменьшим данные квадратики так, что их стороны попадут в
нижний край своего промежутка, т.е. длина стороны квадратика из Ai после
уменьшения будет равна 1/2i. Заметим, что суммарная площадь
новых квадратиков больше 1, т.к. стороны прежних квадратиков уменьшались
менее чем в два раза.
2. Если некоторое множество Ai (1≤і)
содержит хотя бы 4 квадратика, то вместо этих 4-х квадратиков будем рассматривать
один квадратик с удвоенной стороной ( 1/2i + 1/2i = 1/2i-1).
Соответственно множество Ai квадратиков уменьшим на 4, а
множество Ai-1 увеличим на 1.
3. Будем применять п.2 к множествам квадратиков до
тех пор пока возможно. В результате в каждом множестве Ai (1≤і)
окажется не более трёх квадратиков. Следовательно, их суммарная площадь не
превышает 3•(1/4 + 1/16 + 1/64 + ....) = 1. Но в п.1 отмечалось, что
суммарная площадь квадратиков больше 1. Следовательно, множество A0
не является пустым и можно покрыть квадрат S квадратом из A0.
Вернуться на главную страницу
к текстам
Решение задача 5.
а)
Если два целых числа при делении на число p дают равные (разные)
остатки, то будем говорить, что они сравнимы (не сравнимы).
a1) Выпишем пары несравнимых чисел из данной последовательности:
(b1,c1),
(b2,c2),…., (bk,ck).
Для пункта a2 требуется выписать (p–1) пар. Но вдруг
процесс записи пар застопорится, т.е. выписано к<(p–1) пар, а все оставшиеся числа
(их осталось 2p–2k–1) попарно сравнимы? Да, это возможно, но легко преодолимо.
Найдём такую пару из уже выписанных, например, (b1,c1),
что и b1, и c1 не сравнимы
с оставшимися числами. Почему такая пара непременно найдётся? Если допустить,
что в каждой паре имеется число, сравнимое с оставшимися числами
последовательности, то получим противоречие: количество сравнимых чисел
k+(2p–2k–1)≥p. Что же мы будем делать с этой выявленной парой
(b1,c1)?
А просто заменим её на две пары: (b1,ax)
и (с1,ay),
где ax и ay – произвольные
числа из оставшихся прежде членов последовательности. Очевидно, что после
указанных «улучшений» мы придём к набору из (p–1) пар несравнимых чисел.
a2) Рассмотрим p числовых последовательностей.
Первая последовательность A1=(a) содержит единственное число, которое осталось
в пункте a1 после выписывания (p–1) пары. Вторая последовательность:
A2=(a,b1,c1) получается
добавлением к первой последовательности чисел из первой пары. Аналогично
A3=(a,b1,c1,b2,c2),
и т.д. до конца
Ap=(a,b1,c1,b2,c2,...,bp-1,cp-1).
Переходим к заключительному этапу.
a3) Для каждой последовательности Ak
из построенных выше справедливо следующее: можно выбрать k попарно несравнимых сумм,
каждая из которых содержит k слагаемых из Ak. Доказательство
проведём индукцией по k. База индукции при k=1 очевидна. Пусть уже утверждение верно
для k (k<p) и докажем его для k+1. Обозначим через S1,S2,...,Sk
попарно несравнимые суммы, содержащие k слагаемых из Ak. Рассмотрим
два набора сумм: первый –
(S1+bk),(S2+bk),...,(Sk+bk)
и второй – (S1+сk),(S2+сk),...,(Sk+сk).
Очевидно, что в каждом наборе
суммы попарно несравнимы. Если бы оказалось, что во втором наборе есть
сумма несравнимая ни с одной суммой первого набора, то мы её бы и добавили
к первому набору и получили требуемое утверждение. Осталось рассмотреть
последюю возможность: каждая сумма второго набора сравнима с некоторой
суммой первого набора. Следовательно разность между суммой сумм первого
набора и суммой сумм второго набора делится на p. Иначе говоря k(bk–сk)
делится на p. Но это невозможно, т.к. (bk–сk)
не делится на p по построению пар (пункт a1), а k<p. Можно отдышаться.
b)
Пусть для чисел k и m, больших 1, утверждение задачи верно. Покажем, что и
для числа n=km оно также верно (фактически это - индукция). Из имеющихся у нас
2km–1 (2k–1≤2km–1) чисел выберем k чисел b1, b2,...,bk,
сумма которых делится на k. Из оставшихся (2m–1)k–1 (2k–1≤(2m–1)k–1) чисел
снова выберем k чисел с1, с2,...,сk,
сумма которых делится на k. И так далее, пока количество оставшихся чисел будет
не меньше, чем 2k–1, т.е. выбранных сумм будет 2m–1. Разделим полученные суммы
на k и частные обозначим через X1, X2,…, X2m-1.
Как мы помним, а это было нашим
предположением, из этих чисел можно выбрать m чисел, сумма которых делится на m.
Осталось умножить эту сумму на k и каждое произведение заменить на первоначальную
сумму (например, b1+b2+....+bk).
Наконец, отметим, что если n – простое число, то утверждение задачи сразу следует из пункта a.
Замечание 1.
Утверждение из пункта b перестаёт быть верным для 2n–2 чисел.
В качестве контрпримера достаточно рассмотреть (n–1) нулей и (n–1) единиц.
Замечание 2.
Утверждение из пункта b очень гармонично дополняет известное
утверждение (доказывается с помощью принципа Дирихле), что среди n произвольных
целых чисел всегда можно выбрать несколько, сумма которых делится на n.
Вернуться на главную страницу
к текстам
Решение задачи 6.
Подгоним показатели степеней (2,3) поближе к (5,7):
a2+b3 =>
a4+b6 =>
a8+b6 =>
b6+a8. Теперь полагаем
с=d=p, a=p4,
b=p2:
 = p.
Таким образом, любое натуральное число p уже можем записать в виде данной дроби.
Теперь будем считать, что p=x/y, где x,y – любые натуральные числа.
= p.
Таким образом, любое натуральное число p уже можем записать в виде данной дроби.
Теперь будем считать, что p=x/y, где x,y – любые натуральные числа.
 . Почему выбрано число 210?
Просто потому, что 210 делится на 2,3,5,7. Теперь легко указать значения a,b,c,d:
a=x4•y101,
b=x2•y68,
c=x•y41,
d=x•y29.
. Почему выбрано число 210?
Просто потому, что 210 делится на 2,3,5,7. Теперь легко указать значения a,b,c,d:
a=x4•y101,
b=x2•y68,
c=x•y41,
d=x•y29.
Вернуться на главную страницу
к текстам
Решение задачи 7.
Пусть а - произвольное рациональное число из промежутка
(1,10). Скажем, что число a определяет следующую бесконечную числовую последовательность:
a1=a, an+1=
 (n=1,2,3,....).
Заметим, что все члены последовательности - рациональные числа - распределяются
по промежуткам (1;2), [2;3), [3;4), [4;5),...., [9;10).
(n=1,2,3,....).
Заметим, что все члены последовательности - рациональные числа - распределяются
по промежуткам (1;2), [2;3), [3;4), [4;5),...., [9;10).
1) Докажем такой факт: если все соответствующие члены
двух последовательностей, определяемых числами a и в, попадают в одинаковые промежутки,
то a = в.
1а) Сначала от противного установим, что при вычислении
очередных членов последовательностей: an+1 и bn+1
либо одновременно происходит деление на 10, либо одновременно деления на 10 не происходит.
Действительно, допустим что 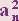 <10 и
10≤
<10 и
10≤ , т.е.
3≤an<bn<4 и
9≤an+1<10, 1<bn+1<2 – противоречие
с предположением.
, т.е.
3≤an<bn<4 и
9≤an+1<10, 1<bn+1<2 – противоречие
с предположением.
1b) Теперь предположим, что a<b и рассмотрим разность
bn–an=
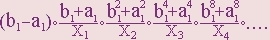 (всего n сомножителей), где каждое Xi равно 1 или 10. Легко
видеть, что начиная с некоторого места все сомножители будут больше 2. Таким образом,
при достаточно большом n имеет место 1<bn–an, что
противоречит принадлежности an и bn одному промежутку.
(всего n сомножителей), где каждое Xi равно 1 или 10. Легко
видеть, что начиная с некоторого места все сомножители будут больше 2. Таким образом,
при достаточно большом n имеет место 1<bn–an, что
противоречит принадлежности an и bn одному промежутку.
2) Перейдём к решению первоначальной задачи. Полагаем
a=2 и рассмотрим соответствующую последовательность a1,
a2,... . Периодичность последовательности первых цифр,
начиная с k-го места и длиной периода t равносильна тому, что соответствующие члены
двух последовательностей ak,ak+1,...
и ak+t,ak+t+1,... попадают
в одни и те же промежутки, а это, как мы уже знаем влечёт ak=ak+t,
чего быть не может, т.к. различные степени числа 2 не могут отличаться множителем вида 10m.
Вернуться на главную страницу
к текстам
Решение задачи 8.
Необходимость выполнения неравенств очевидна.
Достаточность докажем индукцией по числу n юношей в группе.
При n=1 утверждение очевидно. Пусть оно уже верно для всех
групп юношей и девушек, если число юношей в группе меньше n. Назовём
подгруппу Ai юношей критической, если |Ai|=|Bi|.
Далее разберём 2 случая: существует или нет критическая подгруппа.
1) Нет критических подгрупп, кроме, возможно, самой группы.
Выберем произвольно одного юношу и женим его на любимой девушке, такая существует,
причём даже ни одна (уж такие у нас юноши в разбираемом случае). Вычеркнем этих
женатиков из их групп соответственно. Причём для оставшихся групп юношей и девушек
условие задачи выполняется, т.к. до вычёркивания имело место строгое неравенство
|Ai|<|Bi| и после удаления из
Bi одной девушки (той самой, которая ушла замуж),
неравенство сохранится, правда вот такое: “≤”. По предположению индукции пора
играть свадьбы.
2) Существует критическая подгруппа A1 юношей.
Понятно, что для групп A1 и B1 выполняются
условия задачи и по предположению индукции юношей и девушек можно переженить, причём
лишних девушек даже не останется. Обозначим через A2 подгруппу всех юношей,
не попавших в A1. Пусть теперь Ai – произвольная
подгруппа юношей из A2. Рассмотрим соответствующую ей
подгруппу девушек Bi, в которой могут оказаться также
девушки из B1. Удалим из Bi тех
девушек (ведь они уже замужем!), которые попали в B1, и новую
подгруппу девушек обозначим через Bi*.
Покажем, что |Ai|≤|Bi*|
и, следовательно, по предположению индукции две группы юношей и девушек A2 и
B2*, что остались после первой серии свадеб, можно также переженить.
К сожалению не обязательно, что все девушки окажутся невестами.
Итак, докажем неравенство. Подгруппе юношей
AiUA1 соответствует
подгруппа девушек BiUB1=
Bi*UB1.
Далее, |Bi*UB1|
=|Bi*|+|B1|, т.к.
ни одна девушка не является членом сразу обеих подгрупп Bi*
и B1. Аналогично, |AiUA1|=
|Ai|+|A1|, и тогда уже
|Ai|=|AiUA1|–|A1|
≤|Bi*U
B1|–|B1|=|Bi*|.
Вот всё и закончилось хорошо: свадьбами.
Вернуться на главную страницу
к текстам
Решение задачи 9.
Это решение мне рассказали. Раскрасим таблицу наподобие шахматной доски
с размером клетки 1/2. Уточним, раскрашивание начинаем с левого верхнего угла. Теперь нужно "увидеть",
что у каждого прямоугольника половина его площади покрывает чёрные клетки, а другая половина –
белые. Надеюсь, что рисунок поможет это понять.  Следовательно, это же верно и для всей таблицы. Разделим таблицу на 4 части: слева, сверху будет
располагаться первая часть с максимально большими целыми сторонами. Внизу под первой частью будет
лежать вторая часть (строка) с такой же целой длиной, как и выше. Справа от первой части находится
третья часть (столбец) с такой же высотой, как у первой части. Наконец, маленький прямоугольник
(если что-то останется) в правом нижнем углу таблицы – это всё, что мы готовы отдать четвёртой
части. Легко видеть, что площадь каждого из первых трёх кусков распределяется поровну между белыми
и чёрными клетками. Следовательно, такова же и участь четвёртой части. А вот это уже невозможно,
если эта часть существует (разберите самостоятельно 2 случая: когда и длина, и высота больше или
равна 1/2, и когда одна из длин меньше 1/2). Таким образом, четвёртая часть не существует, а значит
не существует вторая или третья часть. А случается это только тогда, когда одна из сторон таблицы –
целое число.
Следовательно, это же верно и для всей таблицы. Разделим таблицу на 4 части: слева, сверху будет
располагаться первая часть с максимально большими целыми сторонами. Внизу под первой частью будет
лежать вторая часть (строка) с такой же целой длиной, как и выше. Справа от первой части находится
третья часть (столбец) с такой же высотой, как у первой части. Наконец, маленький прямоугольник
(если что-то останется) в правом нижнем углу таблицы – это всё, что мы готовы отдать четвёртой
части. Легко видеть, что площадь каждого из первых трёх кусков распределяется поровну между белыми
и чёрными клетками. Следовательно, такова же и участь четвёртой части. А вот это уже невозможно,
если эта часть существует (разберите самостоятельно 2 случая: когда и длина, и высота больше или
равна 1/2, и когда одна из длин меньше 1/2). Таким образом, четвёртая часть не существует, а значит
не существует вторая или третья часть. А случается это только тогда, когда одна из сторон таблицы –
целое число.
Второе решение (ФШ).
1) Сначала расправимся с каждым "большим"
прямоугольником, а именно, если длины его сторон x и y, и 1<x, то разрежем его на два прямоугольника:
(x–1)×y и 1×y. После многократного применения этой процедуры у каждого прямоугольника будет сторона
с длиной 1.
2) Теперь многократно будем применять два вида преобразований: a) если два
прямоугольника соседствуют вдоль общей стороны длины 1, то объединим их, ну а если длина суммарной
стороны превышает 1, то как в пункте 1, разрежем на квадрат 1×1 и то, что останется. b) Если квадрат
1×1 и прямоугольник соседствуют вдоль общей стороны длины 1, то поменяем их местами так, чтобы квадрат
подвинулся вверх или влево. Заметим, что в результате первой операции либо уменьшится число
прямоугольников, либо их число останется прежним, но увеличится число квадратов 1×1. Если применяются
лишь операции второго типа (число квадратов 1×1 остаётся неизменным), то уменьшаться будет сумма
расстояний от центров квадратов до левой и верхней сторон таблицы. Таким образом, применив указанные
операции достаточное число раз, непременно придём к ситуации, в которой операции уже неприменимы.
Оказывается, мы получим те же 4 части, что в решении 1. Причём первая часть покрыта квадратами 1×1,
а вот четвёртая часть(если она существует) не является прямоугольником со стороной 1, что противоречит
условию.
Итак, остаётся доказать, что первая часть заполнена квадратами 1×1.
Рассмотрим то место в таблице, которое должен был занять квадрат 1×1, но не занял. Таких мест может
быть много, но мы выберем его так, что уже слева и сверху от него находятся квадраты 1×1 (или край
таблицы). Можно допустить (без ограничения общности), что к левому верхнему углу несостоявшегося
квадрата примыкает прямоугольник (1) горизонтального вида (высота меньше длины основания), к нему
уже не может примыкать прямоугольник горизонтального вида или квадрат 1×1, следовательно, следующий прямоугольник (2) будет вертикального вида. К (2) уже не может примыкать
прямоугольник вертикального вида или квадрат 1×1, следовательно, следующий прямоугольник (3) будет
горизонтального вида. И так далее без конца. Противоречие.
следовательно, следующий прямоугольник (2) будет вертикального вида. К (2) уже не может примыкать
прямоугольник вертикального вида или квадрат 1×1, следовательно, следующий прямоугольник (3) будет
горизонтального вида. И так далее без конца. Противоречие.
Вернуться на главную страницу
к текстам
Решение задачи 10.
Покажем, что неравенство справедливо,
если n=30000. Действительно, 30000<215, следовательно,
n2000=300002000
<(215)2000=2n.
Первое решение.
Полагаем теперь 30000<n и рассмотрим n следующих
положительных чисел: первые 30000 из них равны n, а последние (n–30000) чисел равны 1. Применим
к этим числам неравенство Коши о среднем арифметическом и среднем геометрическом n положительных
чисел и получим:  откуда немедленно получается
требуемое неравенство.
откуда немедленно получается
требуемое неравенство.
Второе решение.
Покажем, что функция f(x)=(x)1/x
убывает при x>4. Рассмотрим вспомогательную функцию g(x)=ln(f(x))=(1/x)lnx. Вычислим
производную g'(x)=(1–lnx)/x2. Очевидно g'(x)<0 при x>4. Таким
образом, g(x) убывает и, следовательно, убывает также функция f(x). Таким образом, выражение
(n)1/n убывает и для n≥30000 выполняется неравенство
(n)1/n≤(30000)1/30000. А неравенство
(30000)1/30000<(2)1/2000 доказано
в начале.
Замечание.
Можно подсчитать, что при n=29000 неравенство задачи уже не
выполняется.
Вернуться на главную страницу
к текстам
Решение задачи 11.
а)
Легко видеть, что после каждого шага сумма чисел в
каждой строке и каждом столбце увеличивается на 1. Следовательно,
эти суммы остаются одинаковыми и равными Т после Т шагов. Таким образом,
нельзя получить таблицу на рис.2. Таблицу на рис.1 получить можно:
достаточно заметить, что каждое из чисел от 1 до n находится в n
клетках таблицы, располагающихся в разных строках и столбцах.
c)
Целесообразно рассмотреть пункт "c" до пункта "b".
Как отмечено в пункте "а" посредством Т шагов
можно от таблицы, заполненной нулями, перейти к таблице с целыми неотрицательными числами,
у которой суммы чисел в каждой строке и каждом столбце равны Т. Но к любой
ли такой таблице можно перейти? Да, к любой. Но прежде, чем доказать это, установим
для таких таблиц вспомогательный факт: если среди
любых n чисел таблицы, взятых из разных строк и разных
столбцов, имеется 0, то Т=0 и вся таблица заполнена нулями.
Действительно, полагаем, что Т>0. Если
в таблице нет положительных
чисел меньших Т, то легко видеть, что в каждой строке и каждом
столбце имеется единственное число отличное от 0, а именно – Т.
Причём располагаются числа равные Т в разных строках и разных
столбцах, а это противоречит предположению, т.к. в таком наборе
чисел нет ни одного нуля. Итак, можно считать, что в таблице есть
числа из промежутка (0,Т). Выбираем одно из
них: a1. В строке, содержащей
a1, найдётся по
меньшей мере ещё одно число из промежутка (0,T) – ведь сумма всех чисел в строке равна Т.
Выберем одно из них (отличное от a1 по месту
жительства, но, возможно, равное a1). Обозначим
новое число через a2. В столбце, содержащем a2,
найдётся по меньшей мере ещё одно число из промежутка
(0,T). Выберем одно из них (отличное от a2 по месту
жительства, но, возможно, равное a2). Так и будем
продолжать то со строкой, то со столбцом до
тех пор пока не придём к очередному числу ak,
которое находится в уже "использованной" ранее
строке (или столбце). Если в "использованной"
строке (аналогично со столбцом) имеется два
выбранных прежде числа (ai-1, ai), то
будем рассматривать цикл чисел ai,ai+1,
..., ak. Если в "использованном" столбце
имеется лишь одно выбранное прежде число
(таким числом будет непременно a1 и строки
сейчас не подходят, т.к. в них всегда есть два
выбранных прежде числа), то цикл начнём именно
с него. Важно отметить, что в построенном цикле
любые 2 соседних числа (первое и последнее
числа также считаем соседними) находятся в
одной строке или столбце. Более того, если два
соседних числа "соседствуют" в строке, то
второе из них и следующее за вторым уже "соседствуют"
в столбце и наоборот, следовательно количество
чисел в цикле – чётное. Теперь найдём в нашем
цикле наименьшее число a=ap и изменим каждое
число aj цикла так: если (j–p) – чётное
число, то уменьшим aj на a, в противном
случае увеличим aj на a. Легко видеть,
что сумма чисел любой строки или столбца
осталась прежняя, а количество нулей в
таблице увеличилось. Этот процесс можно
продолжать неограниченно. Но количество
нулей в таблице не может превышать числа
клеток в таблице. Следовательно, T=0 и
таблица заполнена нулями. Вспомогательный факт доказан.
Пусть теперь задана таблица n×n, заполненная
целыми неотрицательными числами, причём суммы чисел в каждой строк и каждом столбце
равны Т. Найдём n положительных чисел в таблице, находящихся в разных строках и столбцах.
Совершим "отрицательный" шаг: уменьшим эти числа на 1. При этом суммы чисел по
строкам и столбцам также уменьшатся на 1 (станут равны Т–1). Будем повторять
"отрицательные" шаги, пока это возможно. Пусть теперь пришли к таблице, у которой
среди любых n чисел, находящихся в разных строках и столбцах, имеется 0. Но выше показано, что
такая таблица заполнена нулями. Таким образом, применив к этой "нулевой" таблице те же шаги, но в сторону
увеличения, получим в результате первоначальную таблицу.
b)
Если данная таблица имеет размеры 2×2, то нет возможности
заполнить её попарно различными числами. А вот для размера n≥3
это возможно, причём многими разными способами. Приведу два способа:
конструктивный и неконструктивный. Начну со второго, т.к. его
проще записать. Набор из n клеток таблицы, взятых из разных строк
и столбцов будем называть набором. Выпишем в некотором порядке
все наборы (всего их n!), заполненные первоначально нулями.
К числам первого набора добавим 1, к числам второго набора
добавим 2, к числам третьего набора добавим 4, к числам
четвёртого набора добавим 8 и т.д. В результате все числа в
таблице будут разными, т.к. для любых двух клеток найдутся
наборы, содержащие одну из клеток и не содержащие другую, а,
следовательно, находящиеся в них суммы разных степеней числа 2,
дадут разные результаты.
Перейдём к конструктивному способу. Построение
разобъём на несколько пунктов.
b1) Временно удалим из таблицы последний столбец
и последнюю строку. Полагаем k=n–1 и наша цель
– заполнить оставшуюся таблицу (k×k) попарно
различными числами так, чтобы суммы чисел по строкам
и столбцам также были попарно различны. Заполнять
будем так: в первую строку запишем числа 1,2,...,k,
во вторую строку – числа k+1,k+2,...,2k, и т.д. Подсчитаем
суммы чисел в строках: A1=k(k+1)/2, A2=k(k+1)/2+k2,
A3=k(k+1)/2+2k2,..., Ak=k(k+1)/2+(k–1)k2.
Также подсчитаем суммы чисел в столбцах: B1=k(k2–k+2)/2,
B2=k(k2–k+4)/2,..., Bk=k(k2+k)/2.
Очевидно, что A1<A2<...<Ak и
B1<B2<...<Bk.
Но не будет ли
совпадений между суммами по строкам и столбцам?
При k=2 все суммы разные. А при 2<k возможно одно
совпадение. Преодолеем это препятствие так: увеличим
все числа в нижней строке на 1. И будем рассматривать
остатки от деления полученных сумм на k, если k –
нечётное число, и соответственно остатки от деления
на k/2, если k – чётное число. Остатки по строкам
равны 0, а по столбцам – 1. Итак, таблица с попарно
различными числами и попарно различными суммами по
строкам и столбцам построена.
b2) Перед возвращением последнего столбца и последней строки
(пока что заполненных нулями) обозначим через x – самое
большое число в таблице, через y – самую большую сумму
среди столбцов и строк, и, наконец, выберем число S так,
чтобы во–первых, x+y<S и, во–вторых, A1+A2+...+An-1≤(n–2)S.
Переходим к заполнению последнего столбца, кроме самой нижней
клетки: S–A1, S–A2, ..., S–An-1. Нижнюю строку, кроме
самой правой клетки, заполним так: S–B1, S–B2,..., S–Bn-1.
Из определения числа S легко видеть, что числа в последнем
столбце и последней строке попарно различны и больше чисел,
находящихся в других строках и столбцах. Наконец, в правый
нижний угол таблицы впишем число z=A1+A2+...+An-1–(n–2)S.
Отметим, что z≤0 и, следовательно, не совпадает ни с одним
другим числом в таблице. Суммы чисел в каждой строке и каждом
столбце равны S (ведь A1+A2+...+An-1=B1+B2+...+Bn-1).
Единственный недостаток построенной таблицы, что, конечно,
мешает нашему эстетическому чувству – это z≤0. Чтобы убрать
этот недостаток достаточно добавить ко всем числам в таблице число 1–z.
Вот как выглядит таблица 5×5, следуя изложенному,
 .
.
Вернуться на главную страницу
к текстам
Решение задачи 12.
а)
Задача эта оказалась для меня очень трудной. Получил я её в 7–м классе, а решил
только в 9–м. Но зато какую радость испытал! И позже рассказал это решение на
кружке при пединституте.
а1)
Сначала заметим, что числа с, a+b+c и 4a+2b+c – целые, т.к. являются точными
квадратами. Отсюда вытекает, что числа с, 2b, 4a также являются целыми. Умножим
трёхчлен на 4 и будем считать целыми числами коэффициенты нового трёхчлена. Но
сохраним прежнюю запись трёхчлена.
а2)
Теперь установим такой факт: b2 делится на с. Пусть p –
произвольный простой делитель с. И пусть, далее, p2k –
наивысшая степень p, на которую делится с (показатель степени – чётный, т.к.
с – точный квадрат). Докажем, что b делится на pk.
Обозначим через pi наивысшую степень p, на которую делится b
(возможно даже, что i=0). Теперь допустим, что i<k и
подставим в трёхчлен x=pi+1. Заметим, что
значение трёхчлена ap2(i+1)+bpi+1+c
делится на p2i+1 и, следовательно, делится на p2i+2,
т.к. является точным квадратом. Но тогда и b делится на pi+1 вопреки определению
(помните: pi – наивысшая степень p, на которую делится
b?). Следовательно, допущение i<k – ложно и на самом деле b
делится на pk. Из доказанного факта вытекает более общий факт:
b2 делится на с. Этот вывод становится некорректным, если с=0.
Но в этом последнем случае доказано что b делится на любое простое число p. А когда такое
возможно? Только, если b=0.
а3)
Пусть m – произвольное целое число. Подставим в данный трёхчлен x+m вместо x:
a(x+m)2+b(x+m)+c≡
ax2+(b+2am)x+(am2+bm+c).
Легко видеть, что новый трёхчлен также удовлетворяет условию задачи. Но тогда
можно применить к нему утверждение из пункта а2: (b+2am)2
делится на am2+bm+c. Следовательно, разность
(b+2am)2–4а(am2+bm+c) =
b2–4ac также делится на am2+bm+c.
Если a≠0 или b≠0 (случай a=b=0 –
тривиальный), то число am2+bm+c может быть сколь угодно
большим при специально подобранных m. А как же быть с установленной делимостью
b2–4ac на am2+bm+c?
Приходим к единственному выводу: b2–4ac=0.
А т.к. a,b,c – целые числа и c – точный квадрат, то существуют целые d и e,
что a=d2, b=2de, c=e2 и, окончательно,
ax2+bx+c≡(dx+e)2.
a4) Ещё немного усилий. В пункте а1 все коэффициенты
трёхчлена умножили на 4, чтобы получить целые коэффициенты. Таким образом, для
первоначального трёхчлена получено выражение ((dx+e)⁄2)2.
Но сейчас достаточно подставить x=0 и x=1, чтобы убедиться в чётности чисел d и e.
b)
Начнём с нескольких замечаний. Во–первых, данная задача
содержится в известной книге (Полиа и Сеге, Задачи и теоремы
из анализа, Наука, 1978, отдел восемь, задача 114).
Во–вторых, нельзя ли (всегда) указать многочлен g(x) с
целыми коэффициентам? Ответ отрицательный, вот пример:
(x(x+1)(x+2)/6)2.
В–третьих, для решения задачи нужно знать основные факты
о многочленах над полем рациональных чисел (их изучают,
в частности, на 2–м курсе пединститутов).
b1) Покажем, что все
коэффициенты f(x) – рациональные числа. Пусть n –
степень f(x). Подставим значения x=0,1,...,n и получим
целые значения f(0),f(1),...,f(n).
По теореме Лагранжа строим многочлен с рациональными
коэффициентами, который принимает такие же значения и
имеет степень не выше n. Ввиду единственности многочлена,
принимающего данные значения и степени не выше n, можно
утверждать, что f(x) – многочлен с рациональными
коэффициентами.
b2)
Простым многочленом я называю многочлен с положительным
старшим коэффициентом, получаемый из неприводимого
многочлена после умножения последнего на наименьший общий
знаменатель всех его коэффициентов и деления всех (уже целых)
коэффициентов на их наибольший общий делитель. Далее, f(x)
можно единственным образом записать в виде произведения
некоторого рационального числа и простых многочленов.
Произведение всех простых многочленов в этом произведении, встречающихся
чётное число раз запишем так: P(x)2.
Окончательно, f(x)=(a/b)P(x)2Q(x),
где a,b – натуральные числа, P(x),Q(x) – многочлены с
целыми коэффициентами, причём среди простых многочленов,
на которые разлагается Q(x), нет одинаковых, т.е.
НОД(Q(x),Q′(x))=1. Легко видеть, что многочлен abQ(x)
также удовлетворяет условию задачи. И именно его далее будем
обозначать через Q(x). Если Q(x) – многочлен нулевой степени,
то требуемое утверждение доказано. Ниже полагаем, что Q(x)
имеет положительную степень.
b3)
Пусть m – натуральное число и Q(m)≠0. Докажем, что
число Q′(m)2 делится на число Q(m). Запишем многочлен
Q(x+m) по степеням x: Q(x+m)=cjxj+...+c2x2+c1x+c0.
Далее повторяем выкладки из пункта а2. Пусть p – произвольный
простой делитель с0. И пусть, далее, p2k – наивысшая
степень p, на которую делится с0 (показатель степени –
чётный, т.к. с0 – точный квадрат).
Докажем, что c1 делится на pk.
Обозначим через pi наивысшую степень p, на которую делится c1
(возможно даже, что i=0). Теперь допустим, что i<k и
подставим x=pi+1 в Q(x+m).
Заметим, что число Q(pi+1+m)=
cjpj(i+1)+...+c2p2(i+1)+c1pi+1+c0.
делится на p2i+1 и, следовательно, делится на p2i+2,
т.к. является точным квадратом. Но тогда и c1 делится на pi+1
вопреки определению (помните: pi –
наивысшая степень p, на которую делится c1?).
Следовательно, допущение i<k – ложно и
на самом деле c1 делится на
pk. Из доказанного факта вытекает
более общий факт: число Q′(m)2=c12
делится на число Q(m)=c0.
b4)
Разделим с остатком многочлен Q′(x)2
на Q(x) и соответствующее равенство умножим на общий знаменатель
коэффициентов: uQ′(x)2=Q(x)A(x)+B(x),
причём коэффициенты всех многочленов – целые числа и степень B(x)
меньше степени Q(x). В частности, существует такое большое число k,
что для всех натуральных чисел m>k имеет место Q(m)>|B(m)|.
Но, ввиду пункта b3, число B(m) делится на число Q(m). Следовательно, B(m)=0. А т.к. количество
таких чисел m ничем не ограничено, то B(x)≡0. Другими
словами Q′(x)2 делится на Q(x).
Но в пункте b2 было установлено, что НОД(Q(x),Q′(x))=1.
Следовательно, Q(x) – многочлен нулевой степени и доказательство закончено.
Вернуться на главную страницу
к текстам
Решение задачи 13.
Разрежем плоскость на квадраты 1×1 с целочисленными вершинами. Будем считать,
что плоскость выполнена из идеально прозрачного стекла, а клякса – чёрная.
Положим все квадраты один на другой, не поворачивая их. Под квадратами зажжём яркую
лампу и глянем на нашу пирамиду сверху. Если мы не увидим ни одной яркой точки,
т.е. все точки (на разных уровнях) покрыты кляксой, то можно утверждать, что площадь
кляксы больше или равна 1. По условию это не так. Следовательно, где то увидим яркие
точки. Для нас достаточно одной точки: пусть её координаты – (a,b), где 0<a<1 и
0<b<1. Склеим снова плоскость и передвинем оси координат параллельно самим себе так,
чтобы новое начало координат пришлось на точку (a,b). Легко видеть, что все точки
с целочисленными координатами не находятся на кляксе, т.к. все они в собранном виде
находились в точке (a,b).
Вернуться на главную страницу
к текстам
Решение задачи 14.
Эту задачу я взял из книги И.М.Яглома "Избранные задачи и теоремы элементарной математики"
(часть 1, задача 109, издание 2, Москва, 1954). Именно эта книга научила меня думать и,
хотя мне не выпала честь знать И.М.Яглома, я считаю его великим методистом и своим Учителем.
Существует ещё одна нередко встречающаяся функция, определённая
для всех действительных чисел и принимающая лишь целые значения: антье [x]= наибольшему
целому числу, не превосходящему x. Далее установим связь между двумя функциями: (x)=[2x]–[x].
Обозначим целое число [x] через m и разберём 2 случая: m≤x<m+1/2
и m+1/2≤x<m+1. В первом случае имеем:
(x)=m, [x]=m и [2x]=2m, т.е. (x)=[2x]–[x].
Соответственно во втором случае: (x)=m+1, [x]=m и [2x]=2m+1,
и снова (x)=[2x]–[x].
А теперь перейдём к задаче:
(n/2)+(n/4)+(n/8)+(n/16)+...=
[n]–[n/2] + [n/2]–[n/4] + [n/4]–[n/8]
+ [n/8]–[n/16] + ... =n.
Идея решения совпадает с той, что использована в моей статье "Ищем суммы".
Вернуться на главную страницу
к текстам
Решение задачи 15.
В доказательстве будем использовать индукцию по числу n. Для n=1 и n=2 утверждение очевидно и
будем предполагать, что оно верно для всех натуральных чисел меньших n. Далее, полагаем,
что 2<n
и a1<a2<....<an,
и M={b1,b2,....,bn-1}, причём
b1<b2<....<bn-1.
Введём ещё обозначения: A={a1,a2,....,an};
Ai получается из A выкидыванием одного числа: ai;
Aij получается из A выкидыванием двух чисел: ai и aj.
Сумму всех чисел из Ai обозначим через Si,
а сумму всех чисел из Aij обозначим через Sij.
Далее, множество Mi получается из M выкидыванием одного числа: bi.
Пусть, наконец, X и Y – два конечных числовых множества. Назовём X критическим (некритическим) относительно Y,
если сумма всех чисел из X содержится (не содержится) в Y.
Назовём X допустимым относительно Y, если можно так перенумеровать члены X: x1,x2,....,xk,
что все частичные суммы: x1, x1+x2,
x1+x2+x3,....,
x1+x2+....+xk
не содержатся в M. Итак, в новых обозначениях нужно показать, что
A – допустимое множество относительно M.
Переходим к доказательству, которое разобъём на несколько пунктов.
1. Пусть Si не содержится в M. По предположению индукции
Ai – допустимое множество относительно Mn-1.
Если допустить, что Si<bn-1,
то (не меняя порядка) добавим к Ai в конце ещё член ai
и получим, что A – допустимое множество относительно M. Таким образом, далее полагаем,
что если Si не содержится в M, то bn-1<Si.
2. Не могут все числа
S1>S2>....>Sn
содержаться в M (по условию в M имеется n–1 число).
Следовательно (пункт 1), S1 не содержится в M, и
A1 – некритическое множество относительно M.
3. Допустим, что An – некритическое множество относительно M,
т.е. a1+a2+....+an-1
не содержится в M. Тогда по предположению индукции An
является допустимым относительно Mn-1.
Т.е. можно так перенумеровать члены An:
y1,y2,....,yn-1,
что среди частичных сумм не встретятся числа
b1,b2,....,bn-2.
Если также не встретится число bn-1,
то все частичные суммы последовательности
(y1,y2,....,yn-1,an)
не содержатся в M и, следовательно, A – допустимое множество относительно M.
Теперь рассмотрим случай: y1+y2+....+yk=bn-1.
Заменим в последовательности (y1,y2,....,yn-1)
число yk на an, а число yk припишем в
конце и отметим, что новая частичная сумма (а также следующие за ней)
y1+y2+....+yk-1+an
уже больше bn-1. Следовательно,
снова A – допустимое множество относительно M. Так что
далее будем предполагать, что An –
критическое множество относительно M.
4. Ввиду пунктов 1–3 можно утверждать, что существует натуральное число m (1<m≤n)
такое , что все числа Sn<Sn-1<...<Sm
содержатся в M, а числа Sm-1<...<S1
не содержатся в M.
5. Рассмотрим m–1 подмножеств
Am-1,n,...., A1,n.
Все они содержатся в An и не могут одновременно
быть критическими относительно M, т.к. не могут n разных чисел
Sm-1,n<....<S1,n<Sn<Sn-1<....<Sm
одновременно находиться в M (числа Sn,Sn-1,....,Sm
находятся в M). Таким образом, существует некритическое множество
Ai,n относительно M, оно получено из
множества A выкидыванием двух чисел: ai и an (1≤i≤m–1).
6a. Допустим, что Si,n<bn-2.
По предположению индукции Ai,n – допустимое
множество относительно {b1,b2,....,bn-3}.
Добавим к последовательности Ai,n справа
сначала число an (получим множество Ai),
а затем добавим и число ai
(получим множество A). Таким образом, A – допустимое множество относительно M.
6b. Допустим теперь, что bn-2<Si,n,
и, далее, bn-2<Si,n<Sn≤bn-1,
т.е. Sn=bn-1 и m=n.
По предположению индукции множество An допустимое
относительно Mn-1. Т.е. можно
перенумеровать числа a1,a2,....,an-1
так: y1,y2,....,yn-1,
что все частичные суммы:
y1, y1+y2,
y1+y2+y3,....,
y1+y2+....+yn-1
не содержатся в Mn-1 (напомню, что последняя сумма равна bn-1).
Но тогда последовательность y1,y2,...,yn-2,an,yn-1
такова, что все её частичные суммы не содержатся в M.
Вернуться на главную страницу
к текстам
Решение задачи 16.
1) Рассмотрим сначала случай, когда a делится на b без остатка.
Полагаем a=bq, тогда b2–q=b2(q2+1)–
(b2q+1)q делится на b2q+1.
Но абсолютная величина |b2–q| меньше, чем
b2q+1. Следовательно, b2–q=0
и a=b3, что уже даёт серию решений. Этот путь можно продолжить,
рассматривая деление с остатком a=bq+r. Так, нетрудно показать, что
 =q+1.
Но мы пойдём другим путём.
=q+1.
Но мы пойдём другим путём.
2) Пусть теперь a>b и a≠b3. Заметим, что
a(a–b3) = a2 + b2
–(ab+1)b2 также делится на ab+1.
Но тогда и a–b3 делится на ab+1.
Однако деление невозможно, если a>b3, т.к.
a–b3<a<ab+1.
Итак, b<a<b3 и b3–a
делится на ab+1. Обозначим теперь
 =k (*).
Отметим, что k<
=k (*).
Отметим, что k< <b и,
кроме того, a<b2. Выразим из (*) a:
<b и,
кроме того, a<b2. Выразим из (*) a:
 (**).
(**).
И далее, (b2+k2)b=(b3–k)+(kb+1)k
делится на kb+1, а тогда и b2+k2
делится на kb+1. Таким образом от пары (a,b) мы перешли к аналогичной паре (b,k),
причём k<b<a. Такой спуск будет продолжаться до тех пор,
пока не придём к паре с условием b=k3.
3) Теперь от спуска переходим к подъёму:
выбираем произвольное натуральное число c1
(c1≠1),
второе число строим так: c2=(c1)3,
а каждое следующее число, начиная с третьего, строим используя равенство (**):
cn+2=((cn+1)3–cn)/(cncn+1+1).
Отметим, что каждые два соседних числа из этой последовательности
удовлетворяют условию задачи. Для забавы построим несколько первых членов
двух первых последовательностей:
c1=2, c2=8, c3=30, c4=112, c5=418,…
c1=3, c2=27, c3=240, c4=2133, c5=18957,…
4) Из (**) легко вывести два равенства:
 . Таким образом,
в каждой последовательности (п.3) отношение
. Таким образом,
в каждой последовательности (п.3) отношение  сохраняет своё значение и оно равно (c1)2, что решает
задачу из п.b.
сохраняет своё значение и оно равно (c1)2, что решает
задачу из п.b.
Вернуться на главную страницу
к текстам
Решение задачи 17.
Пересчитаем камни в кучках: A≤B≤C.
1) Пусть A+B+C – чётное число. Если все три числа – чётные, то
ситуация проигрышная, т.к. второй игрок будет повторять ходы
первого и всегда ситуация с тремя чётными числами предстаёт
перед первым игроком. В частности, ситуация с двумя 0 тоже
ожидает первого игрока. Если среди трёх чисел A,B,C только одно
чётное, то ситуация наоборот выигрышная, т.к. первый игрок
легко переходит к трём чётным числам, а далее уже ход второго
игрока.
2) Пусть A+B≤C. Если A и B – чётные числа, то ситуация
проигрышная, т.к. второй игрок всегда может вернуть эту
ситуацию, повторяя ход первого игрока. Таким образом,
ситуация с двумя 0 тоже ожидает первого игрока. Если среди
чисел A и B имеется нечётное число, то ситуация наоборот
выигрышная, т.к. первый игрок сможет восстановить чётность
чисел A и B, если потребуется, взяв камень из третьей кучки.
3) Остался последний случай, когда A+B+C – нечётное число и
A≤B≤C<A+B. Пусть r – остаток от деления A+B+C на 4.
Вот ответ в этом случае: если r=1, то выиграет второй игрок,
если r=3, то выиграет первый игрок.
Доказательство проведём индукцией по числу A+B (Сразу для всех
допустимых A и B). Но сначала уточним идею доказательства:
при КАЖДОМ ходе "проигрыш" заменяется на "выигрыш",
а "выигрыш" МОЖНО заменить на "проигрыш" при некотором ходе.
База индукции. A=1, B=1 и тогда C=1. Ситуация выигрышная и
r=3. (Ситуация A=0, B=1 не относится к п.3, т.к. 1=B≤C<A+B=1).
Шаг индукции. Пусть для всех ситуаций с меньшей, чем A+B,
суммой младших чисел утверждение (r=1 – "проигрыш", r=3 – "выигрыш")
справедливо. Рассмотрим ситуацию с числами A,B,C, причём
1≤A≤B≤C<A+B, A+B+C – нечётное число.
После одного хода возможны три ситуации: (A-1,B-1,C),
(A-1,B,C-1), (A,B-1,C-1), причём во второй ситуации B<C,
в третьей ситуации A<B. Если эти ситуации относятся к п.3, то
всё доказано ввиду предположения индукции. Первая ситуация
выходит за рамки п.3 тогда, когда A-1+B-1≤C. Но C<A+B,
следовательно, C=A+B-2 или C=A+B-1. Первое равенство не может
иметь место, т.к. A+B+C – нечётное число, т.е. C=A+B-1.
И далее, A+B+C=2(A+B)-1.
Если r=1 ("проигрыш") у первоначальных чисел,
то A+B - нечётное число, и среди чисел A-1 и B-1 имеется
нечётное число. Следовательно, ситуация A-1,B-1,C - выигрышная
(п.2).
Для случая r=3 ("выигрыш") нужно рассмотреть редкую
возможность, когда ни второй ситуации, ни третьей ситуации не
существует, т.е. A=B=C. Но первая ситуация A-1,A-1,A относится
к п.3, причём r=1 и имеет место "проигрыш". Всё.
Вернуться на главную страницу
к текстам
Решение задачи 18.
Вместо каждого числа x в первоначальной строке будем рассматривать пару чисел
(a,x), где a – номер числа x в строке (назовём a первой компонентой
пары, а x – второй компонентой). Множество всех пар обозначим через S.
Будем говорить, что пара (a,x) меньше пары (b,y) (или иначе (b,y) больше (a,x)),
если a<b и x<y.
Примеры: пара (4,7) меньше пары (6,11), а пары (4,11) и (6,9) несравнимы, т.к. ни одна
не меньше другой. Наконец, скажем, что пара (a,x) – минимальная, если
нет меньших её пар. Множество всех минимальных пар в S обозначим через A1.
Все пары в A1 не сравнимы друг с другом,
следовательно, если первые компоненты пар возрастают (а это соответствует порядку
вторых компонент в первоначальной строке), то вторые компоненты убывают, а если
их количество превышает n, то уже найдена убывающая последовательность
в первоначальной строке, содержащая n+1 число.
Пусть теперь в A1 не более n пар. Выбросим из S
все пары, которые находятся в A1 и это множество
пар обозначим через S1.
Отметим, что для каждой пары из S1 найдётся меньшая
пара в A1. Поступим с S1 аналогично.
Выделим там множество минимальных пар и обозначим его A2.
Все пары в A2 несравнимы друг с другом, следовательно,
если первые компоненты возрастают (а это соответствует порядку вторых компонент
в первоначальной строке), то вторые компоненты убывают, а если их количество
превышает n, то уже найдена убывающая последовательность в первоначальной
строке, содержащая n+1 число.
И т.д. будем строить множества S,S1,S2,…,Sn.
Если каждое из множеств A1,A2,…,An содержит не более n пар,
то множество Sn≠ø. Выбираем в Sn
произвольную пару (x,an+1), затем выбираем в An меньшую пару (y,an)
и т.д. до пары (z,a1) в A1. И получили последовательность чисел
a1<....<an<an+1 из первоначальной строки.
Рассмотрим таблицу
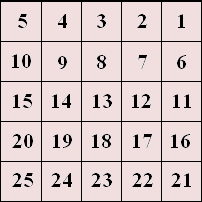 и выпишем одна за другой строки этой таблицы.
Числа из разных строк возрастают, но числа из
одной строки убывают. Следовательно, нельзя
выбрать 6 убывающих или возрастающих чисел.
Аналогично можно построить пример для
произвольного n.
и выпишем одна за другой строки этой таблицы.
Числа из разных строк возрастают, но числа из
одной строки убывают. Следовательно, нельзя
выбрать 6 убывающих или возрастающих чисел.
Аналогично можно построить пример для
произвольного n.
Вернуться на главную страницу
к текстам
 = p.
Таким образом, любое натуральное число p уже можем записать в виде данной дроби.
Теперь будем считать, что p=x/y, где x,y – любые натуральные числа.
= p.
Таким образом, любое натуральное число p уже можем записать в виде данной дроби.
Теперь будем считать, что p=x/y, где x,y – любые натуральные числа.
 . Почему выбрано число 210?
Просто потому, что 210 делится на 2,3,5,7. Теперь легко указать значения a,b,c,d:
a=x4•y101,
b=x2•y68,
c=x•y41,
d=x•y29.
. Почему выбрано число 210?
Просто потому, что 210 делится на 2,3,5,7. Теперь легко указать значения a,b,c,d:
a=x4•y101,
b=x2•y68,
c=x•y41,
d=x•y29.
 (n=1,2,3,....).
Заметим, что все члены последовательности - рациональные числа - распределяются
по промежуткам (1;2), [2;3), [3;4), [4;5),...., [9;10).
(n=1,2,3,....).
Заметим, что все члены последовательности - рациональные числа - распределяются
по промежуткам (1;2), [2;3), [3;4), [4;5),...., [9;10).
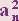 <10 и
10≤
<10 и
10≤ , т.е.
3≤an<bn<4 и
9≤an+1<10, 1<bn+1<2 – противоречие
с предположением.
, т.е.
3≤an<bn<4 и
9≤an+1<10, 1<bn+1<2 – противоречие
с предположением.
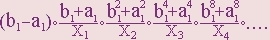 (всего n сомножителей), где каждое Xi равно 1 или 10. Легко
видеть, что начиная с некоторого места все сомножители будут больше 2. Таким образом,
при достаточно большом n имеет место 1<bn–an, что
противоречит принадлежности an и bn одному промежутку.
(всего n сомножителей), где каждое Xi равно 1 или 10. Легко
видеть, что начиная с некоторого места все сомножители будут больше 2. Таким образом,
при достаточно большом n имеет место 1<bn–an, что
противоречит принадлежности an и bn одному промежутку.
 Следовательно, это же верно и для всей таблицы. Разделим таблицу на 4 части: слева, сверху будет
располагаться первая часть с максимально большими целыми сторонами. Внизу под первой частью будет
лежать вторая часть (строка) с такой же целой длиной, как и выше. Справа от первой части находится
третья часть (столбец) с такой же высотой, как у первой части. Наконец, маленький прямоугольник
(если что-то останется) в правом нижнем углу таблицы – это всё, что мы готовы отдать четвёртой
части. Легко видеть, что площадь каждого из первых трёх кусков распределяется поровну между белыми
и чёрными клетками. Следовательно, такова же и участь четвёртой части. А вот это уже невозможно,
если эта часть существует (разберите самостоятельно 2 случая: когда и длина, и высота больше или
равна 1/2, и когда одна из длин меньше 1/2). Таким образом, четвёртая часть не существует, а значит
не существует вторая или третья часть. А случается это только тогда, когда одна из сторон таблицы –
целое число.
Следовательно, это же верно и для всей таблицы. Разделим таблицу на 4 части: слева, сверху будет
располагаться первая часть с максимально большими целыми сторонами. Внизу под первой частью будет
лежать вторая часть (строка) с такой же целой длиной, как и выше. Справа от первой части находится
третья часть (столбец) с такой же высотой, как у первой части. Наконец, маленький прямоугольник
(если что-то останется) в правом нижнем углу таблицы – это всё, что мы готовы отдать четвёртой
части. Легко видеть, что площадь каждого из первых трёх кусков распределяется поровну между белыми
и чёрными клетками. Следовательно, такова же и участь четвёртой части. А вот это уже невозможно,
если эта часть существует (разберите самостоятельно 2 случая: когда и длина, и высота больше или
равна 1/2, и когда одна из длин меньше 1/2). Таким образом, четвёртая часть не существует, а значит
не существует вторая или третья часть. А случается это только тогда, когда одна из сторон таблицы –
целое число.
 следовательно, следующий прямоугольник (2) будет вертикального вида. К (2) уже не может примыкать
прямоугольник вертикального вида или квадрат 1×1, следовательно, следующий прямоугольник (3) будет
горизонтального вида. И так далее без конца. Противоречие.
следовательно, следующий прямоугольник (2) будет вертикального вида. К (2) уже не может примыкать
прямоугольник вертикального вида или квадрат 1×1, следовательно, следующий прямоугольник (3) будет
горизонтального вида. И так далее без конца. Противоречие.
 откуда немедленно получается
требуемое неравенство.
откуда немедленно получается
требуемое неравенство.
 .
.
 =q+1.
Но мы пойдём другим путём.
=q+1.
Но мы пойдём другим путём.
 =k (*).
Отметим, что k<
=k (*).
Отметим, что k< <b и,
кроме того, a<b2. Выразим из (*) a:
<b и,
кроме того, a<b2. Выразим из (*) a:
 (**).
(**).
 . Таким образом,
в каждой последовательности (п.3) отношение
. Таким образом,
в каждой последовательности (п.3) отношение  сохраняет своё значение и оно равно (c1)2, что решает
задачу из п.b.
сохраняет своё значение и оно равно (c1)2, что решает
задачу из п.b.
 и выпишем одна за другой строки этой таблицы.
Числа из разных строк возрастают, но числа из
одной строки убывают. Следовательно, нельзя
выбрать 6 убывающих или возрастающих чисел.
Аналогично можно построить пример для
произвольного n.
и выпишем одна за другой строки этой таблицы.
Числа из разных строк возрастают, но числа из
одной строки убывают. Следовательно, нельзя
выбрать 6 убывающих или возрастающих чисел.
Аналогично можно построить пример для
произвольного n.